On this page
-
Text (3)
-

Untitled Article
-
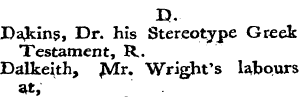
Untitled Article
-
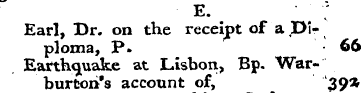
Untitled Article
Note: This text has been automatically extracted via Optical Character Recognition (OCR) software. The text has not been manually corrected and should not be relied on to be an accurate representation of the item.
-
-
Transcript
-
Note: This text has been automatically extracted via Optical Character Recognition (OCR) software. The text has not been manually corrected and should not be relied on to be an accurate representation of the item.
Additionally, when viewing full transcripts, extracted text may not be in the same order as the original document.
Untitled Article
On the £ pir & of JteJigious Cpsx troversy , I 46 . His reply to . A ** LyCONSTAHT Ri ^** , « £ tfc * Trinity . 614 , Controversy , Religious , 09 the gpjtrit of , Copping , Mr . Cornwailis , Dr .
CORRESPONDENCE , 56 , izo , 176 , Z 45 , 3 ° s » 354 * 4 i 4 t 473 s 529 , 586 , 649 , 706 . Cottage , The , Country Schoolmaster , A , to the Authors of the Improved Version , Couper in Fife , Mr . Wright preaches in the Weaver ' s Hall at ,
Coveney , Miss , O . Co vent-Garden Theatre , account of the riots at !! , 525 , 580 , 645 , joz . Crain , a Mohawk Indian , his Speech to the Missionaries , Crief , Mr . Wrieht preaches in the Weavers * Hall , at ,
Critical Review , aoo , 419 Crito ' s Defence of Unitarianisni and refutation of Trinitarianism , i * 5 * Curwen , Mr . his definition of a true Whig , Cyprian Baraza , Father , his Method r of converting the Indians ,
Untitled Article
^ M * E X , * ft ?
Untitled Article
r > . Dajdns , Dr . his Stereotype Greek Testament , R . Dalke ^ th , £ £ r . Wright ' s labours at , Dancer , Daniel , aoa , Dayies , Rev . David , his Sermon
on Jesus the Son of Joseph , R , 509 . His Letters on the Miraculous Conception * R . DeatH , ^ Suaaen , not any evil to r £ ood men , lie Foe , On the character of , DemeraraJ ^ Ifej & ion , pj $ nne , Mr . some account of , Devil , on the existence of the , 134 ,
431—433 . Extent of his power ,, T 36 , aftft . jN . uj ^ b < er of times in which , the W $ r 4 , occurs in Scripture , 136 . Passages alluding to his existence , 436 , Passages supfoumg hif « .. t » « ayp access Xo the human mind , ib . Passages yv- ^^ rein . the same > vor 4 is used in jits original and proper sense , , 437 . His great cunning ' in peopling thcWettcra Hemisphere ,
Untitled Article
* Biaiogutf" fcetweci a' clerical "tii ugistrate and an Unitariari J 4 'jY . On Endless , Punishment , > 599 yit -O- ^ V account of irflss Price , Of * "
107 . Account of , Mr . Tinck-140 nell , O ., 113 . His Report o£ 48 ^ . the Wiltshire Conference of ^ e-43 ^ neral Baptists , 458 Dilemnia , a Theological one , 8 4 Dillwyn , Wm . his Remarks on
the Civilisation of the Indian ? 3 O 2 in N . America , v *? % DjSCIPJLE OF THE OtD ScHOOX ., Aj On Christian Idolatry , 661 260 Discipline of a Qhrjstian Community , Letters on die , 17 , 85 , 19 a ^ 16 Discourse on the Being of a Go < J , « 1 « 454 350 dissent , reasons for , ^* 7 Z 6
Dissenting Clergy , conjectures respecting their conduct on % hp Fast-day , ^ 33 Dissenters , Evangelical ' , indulge a ^ i 407 illiberal and censorious spirit , 76 . Make the Bible a Stalling-516 horse for absurdity , 77 . Whether the pres ent is the most
favourable time for an application . v to Parliament respecting the Test 31 a Laws , a © 9 , 162 , 333 , 36 $ , 3 7
Dairy , Mr . Wright preaches in the 383 open air at , ^ 515 Drummoni , Rev . T . his . Dfs-516 course on the Origin of Pvil , R . 556 5 to . On the refusal of burial to the Children of Unitarians , v 59 6 Duel , between a noble adulterer arid his brother-in-law , 347
635 Duelling , remarks on , . s %$ Duncannon ' s , E . Xines tp Liber-151 ty , * . 637 345 Dundee , Mr . Wright ' s labours at , 516 4 oz Dunsford , Mr . ' 33 s 368
Untitled Article
E . Earl , Dr . on the receipt of a . Diploma , P * 00 Eanho ^ uake at Lisbon , Bp . Warburton ' s account of , 39 * Eaton , David , his Scripture the only Guide to Religious
Truth : A Narrative , & c . sad edition - % . 68 a , ^ Mr . JLindseyV ; Letter to , f ' £ 8 $ Ebionites , "''" ' ' 7 4 " * 5 ii «| ax 635 Echo , from Herder ' s Paramythin , \ ±%
-
-
Citation
-
Monthly Repository (1806-1838) and Unitarian Chronicle (1832-1833), Dec. 2, 1809, page 757, in the Nineteenth-Century Serials Edition (2008; 2018) ncse.ac.uk/periodicals/mruc/issues/vm2-ncseproduct282/page/5/
-